Tracking Down Solutions

Mathematical modeling is a great way to capture important behaviors of physical systems. Much work goes into researching and understanding how to construct the model. But once that has been done, the concepts that are encoded in its algebra and equations of motion can be used to make measureable predictions. Those predictions, in turn, can be verified by experiment and used to either make better physical systems or change the model to reflect new understanding.

What your car does on the track is called behavior. The behavior of a model describes what happens under what circumstances. Sometimes, behavior is more than a description. It can be measured. Not all behavior is easily measured. Just think about drift. But much is. That behavior which is measureable, we want to model.

What kind of behavior is measureable? Certainly, speed and finish time are measureable in a real race with the right physical instruments. But so are all the forces on the car and its energy uses. But these measurements would be difficult to make on a real car. They and many others can be measured virtually through modeling.

A Model For The Grand Prix Race

Examination of a Grand Prix car's physical behavior on a Grand Prix track yielded three primary models and a general energy equation that can be used with arbitrary track shapes in computer simulations.

1. The model summarized here incorporates dynamic parameters of a race with no drift. Forces include weight, Wheel inertia, axle friction, tread friction, and aerodynamic drag. This model consists of a few sets of closed equations describing the track, car, weight distribution to the axles and two describing the dynamic motion first on the ramp, then on the straight away. Computations based on this model lead to good estimates of car behavior, noteably, time and speed at the finsh line.
2. A second model describes the complex nature of drift and the resulting loss of energy through various types of collisions. Because of the random, catastrophic behavior modeled, only limits were derived. Enumeration of possible spurious events lent itself to devising strategies to avoid problems.
3. A third model provides a structure for investigating vibrational modes of the car wheels about their axles. Critical limits for the onset of such vibrations were calculated and a strategy developed to eliminate concern over this condition.

Though most of the physical aspects of the race were examined to produce these models, some effects were found too small to make a difference. For example, the rotational inertia of a car body though examined, was not included in the closed dynamic parameters model. On the other hand, some aspects can not be modeled in a simple closed system but require iterative solutions on a case-by-race basis. Race dynamics on a curved ramp/flat transition are one example.

The Model Parameters And Expressions

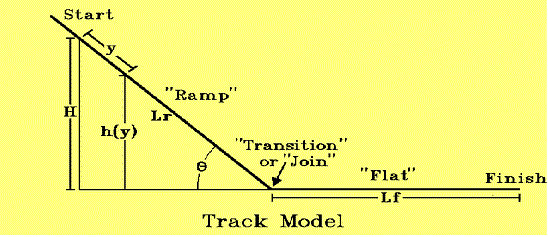
Many kinds of measurements are needed to model a Grand Prix race. These parameters describe the track, your car and the physics between them. The following tables summarize a "simple" behavior model for a Grand Prix race. This model was constructed from two parts. A ramp part and a flat part as shown below. The transistion between the two is an angular join (that is, not a smooth transition) so its effect on the behavior of the race can be minimized. Equations of motion for general angular joins between ramps and catenary transitions are developed in this manual to study transition effects by computer.

In order to present a physically correct model below, the energy lost at the abrupt transition has been included as a cosO factor in the equation for the initial speed on the flat, v0. If you want to use this summary to calculate dynamics closely simmulating a smooth transition track, set that cosO term to the value one (1.0) - only in the v0 equation. The energy loss at the abrupt angular join can be quite high, but on a smooth transition the energy loss (due to ill positioned weight and centrifugal force) is much less.

Below, the most relevant parameters, equations and relationships are presented.

Physical Constants

Though air density and gravitational acceleration are not strickly constants, they are treated as such in this model.

Grand Prix Track Model Parameters

The first four track parameters should be changed to be those of your Grand Prix track. The rest are defined in terms of these. Measurements from the Official AWANA Grand Prix track were used as default values.

Grand Prix Car Model Parameters

Some of the following car parameters are easily measured. Others like the moment of inertia of a wheel are not. This manual contains means by which they can be determined. Default values reflect those of AWANA Grand Prix cars.

Ramp Dynamics Model

A few of the ramp parameters like M, D and D1 are defined to make the expressions clearer and shorter. All are defined in terms of the track and car parameters above. Their values change with those parameters, so they have no defaults. Each expression has a meaningful physical interpretation.

Work of aerodynamic drag

      / y
Wa = | apAv(y)2dy/2
    / 0

Note: arccosh(X) = ln(X+\[XX-1])

Note: tanh(X) = (e^X - e^-X)/(e^X + e^-X)

Flat Dynamics Model (Coasting)

Some of the symbols used in the flat track expressions are ramp parameters. All are in terms of track and car parameters. Note the expressions that measure coasting behaviors.

Finish Line And Maxima

For race results, the ramp and flat equations must be used properly. The car's trajectory must be used on the ramp and flat. This means using trajectory lengths instead of the track lengths, but the same angle for the ramp. Parameters from the track, car, ramp and flat are all used.

With these expressions, a virtual race between two or more cars can be run. Each car can be placed using its time. Intervals between cars are estimated from time difference and the slower speed. That is,

interval = time_difference*slower_speed

Here the time_difference is that between the fastest car and one of the slower ones in the virtual race (slower time minus fastest time). The slower_speed is that of the slower car. So the interval is how far behind the slower car was when the fastest car crossed the finish line. This is a good estimate upto a couple of feet, unless one of the cars is reaching its coasting distance limit and almost stopping on the finish line.

Conclusion

By breaking up the simplified Grand Prix track into two parts, we get a close look at the differences in accelerations, speeds and times and at the differences in the math it took to get there. The equations are very similar with hyperbolic versions of the functions occuring on the ramp part and trigonometric ones on the flat part. Also, because of the initial velocity on the flat track, we got the coasting distance and time with no extra effort.

Notice that if the friction was so high that the coasting distance had been less than the length of the track, our equations would have "broken down" and the "real" car would have stopped on the track. The time function for the finish line would have broken down. Its arccos function has exp((L2-yc)/LM) as an arguement. L2-yc would have been greater than zero making the exp function greater than one. The arccos function is not defined for numbers greater than one. Therefore, the time of the race could not be determined with that expression; the race time is infinite! There are other situations like this where an expression is not valid. For reasonable values of the parameters, this is not a problem. But knowing what "reasonable" is may be.

Is this track model realistic? Yes, it is actually quite good. When used without the correction for energy loss at the abrupt join to simulate a smooth transition (which most tracks have) it matches kinematic computer results and actual race times pretty closely. Since the many factors and behaviors of drift are not included in this model, one expects the calculated times to be less than actual race times. The times might also be less because a smooth transition generates centrifugal force and affects the distribution of this higher axle force to the front and rear wheels differently depending on the balance point. The difference in times can provide clues about the importance of drift and the slightly increased transition friction in the race.

In addition, some factors were not included in this model because they were found to make very little difference and would have required more terms and complexity to calculate. They are examined in the content of this manaul. All of these model expressions and the two other models mentioned above are derived in this manual also.

There is help for evaluating these model equations.