| Grand Prix Racing - | The Science of Fast Pinewood Cars |
This model demonstrates the behavior of a single wheel rolling down a track. It is the first step toward understanding what wheels really do for your car. To keep things simple, no friction is allowed between the wheel and the track. This is almost the situation encountered if a wheel were to roll down a ramp made of ice. If the wheel were to continue on to a flat frictionless surface, it would move across it at the same speed it had at the bottom of the ramp. Because of this, no flat runout is considered.

| E | Energy |
| Ft | Force along the ramp |
| m | Mass |
| g | Acceleration by gravity |
| L | Length of ramp surface |
| y | Distance measured from the top of the ramp surface |
| O | 'Theta', angle the ramp forms with horizon |
| t | Time from starting line |
| a | Acceleration of the wheel |
| v | Speed of the wheel |
| w | Angular speed of the wheel |
| I | Moment of inertia of the wheel |
| r | Outer radius of the wheel |
Important expressions derived for this model include:
| Energy Relation on ramp | E = -mgLsinO = -mg(L-y)sinO + mv2/2 + Iv2/2r2 |
| Equations of Motion on ramp | Ft = m a = -m2gsinO/(m + I/r2) |
| Time on ramp | t(y) = \[-2y(m + I/r2)/mgsinO] |
| Speed on ramp | v(t) = -mgsinOt/(m + I/r2) |
| Position on ramp | y(t) = -mgsinOt2/2(m + I/r2) |
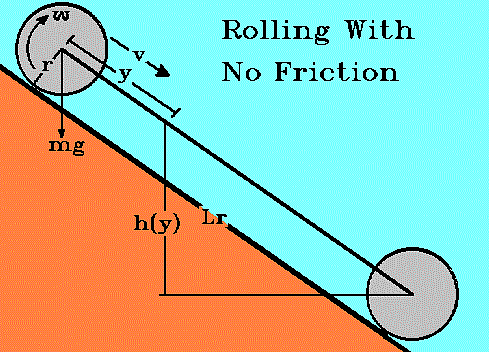
A wheel with radius, r, is rolling down a ramp.
Because it is round, the arc distance traveled per unit time, linear speed, is,
v = rw
The height on the ramp is given as in the other models. O, theta, is negative because the wheel rolls downward.
h(y) = -(L - y)sinO
The energy relation includes the potential energy as well as two terms for the kinetic energy. The first term in v is the linear kinetic energy. The second in w is the rotational kinetic energy.
E = -mgLsinO = mgh + mv2/2 + Iw2/2
Substitute h(y) for h and v/r for w.
E = -mgLsinO = -mg(L-y)sinO + mv2/2 + Iv2/2r2
Add the potential to both sides and collect terms in v.
-mgysinO = v2(m + I/r2)/2
Solve for v2.
v2 = -2mgysinO/(m + I/r2)
Take the square root.
v(y) = \[-2mgysinO/(m + I/r2)]
v(y) = dy/dt in terms of y, so separate the variables in y and t and integrate to get y(t).
/ y / t
| dy/\[y] = \[-2mgysinO/(m + I/r2)] | dt
/ 0 / 0
/ y
The left hand side has the form | dy/\[y] which is 2\[y].
/ 0
/ t
| dt = t
/ 0
so
2\[y] = \[-2mgysinO/(m + I/r2)]t
Divide through by the square root on the right to get t in terms of y,
t(y) = \[-2y(m + I/r2)/mgsinO]
Square both sides.
t2 = -2y(m + I/r2)/mgsinO
Solve for y.
y(t) = -mgsinOt2/2(m + I/r2)
Acceleration in terms of time can be found a couple of ways. First, use the energy relations. Note that the law of conservation of energy requires E to be constant for a conservative force like gravity.
E = -mgLsinO = -mg(L-y)sinO + mv2/2 + Iv2/2r2 = constant, so
This makes it possible to find the time derivative of each term.
dE/dt = -dmgLsinO/dt = -dmg(L-y)sinO/dt + d(mv2/2)/dt + d(Iv2/2r2)/dt
The result is,
dE/dt = 0 = mgsinOdy/dt + mvdv/dt + Iv(dv/dt)/r2
Then since dy/dt = v and dv/dt = a,
dE/dt = 0 = mgvsinO + mva + Iva/r2
Subtract the potential from each side.
mva + Iva/r2 = -mgvsinO
collect terms in av.
av(m + I/r2) = -mgvsinO
Solve for a.
a(t) = -mgsinO/(m + I/r2)
Another way to get the acceleration and speed in terms of time is to plug y(t) into v(y). The first result is the speed in terms of time. Take the time derivative of this speed and the acceleration in terms of time pops out.
v(y) = \[-2mgysinO/(m + I/r2)]
y(t) = -mgsinOt2/2(m + I/r2)
Substitute y(t) for y in v(y).
v(t) = \[m2g2sin2Ot2/(m + I/r2)2]
Take the negative branch when evaluating the square root \[..]
v(t) = -mgsinOt/(m + I/r2)
Take the time derivative of v(t).
dv(t)/dt = -d(mgsinOt/(m + I/r2))/dt
Here it is.
a(t) = -mgsinO/(m + I/r2)
Multiply by mass, m, to get the equation of motion along the ramp.
Ft = m a = -m2gsinO/(m + I/r2)
The force in the normal direction cancels, so
Fn = m a = mgcosO - mgcosO = 0
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |