| Raingutter Boat Racing - | Breathing Life Into Your Boat |
When breath gives out, the hydroplane begins to decelerate. It does so according to a similar model as a Grand Prix car at the flat run out at the end of its track. But once the boat slows enough, the surface tension of the water can no longer hold it and it falls through the surface into the water. This brings the boat to fast stop.
We will only attempt to model the slowing down that occurs while still hydroplaning. The sliding boat begins with this motion energy; mv02/2. v0 is its initial speed. It is found by using the distance traveled during a breath, L, in the acceleration expression for v(y) from the acceleration model.
v0 = v(L) = vt \[1-exp(-epAL/m)]
Mathematical models use mathematical notation. The various environmental, structural and performance factors are written using short one or two letter symbols. Each factor also has physical units that relate to physical measurements that might be measured given appropriate instruments when possible. The table below presents the notations of the factors modeled.
| Symbol | Units | Description |
|---|---|---|
| S | in2 | Area of sail |
| B | in/s | Velocity of breath hitting sail |
| R | oz | Force of air on front of sail resisting motion |
| e | scalar | Coefficient of pressure drag by air on front of sail |
| D | oz | Force of water on hull resisting motion |
| n | scalar | Sliding friction coefficient (on water) |
| m | ozs2/in | Mass of the boat |
| v0 | in/s | Initial velocity of boat |
| L | in | Length of raingutter |
| p | ozs2/in4 | Mass-density of air |
| g | in/s2 | Acceleration by gravity |

Suppose a hydroplane was given an initial speed in a race. How far would it travel before it stopped? How long would it take it? We will begin with the equations of motion. The equations of motion are a special case of the equations of motion for the accelerating hydroplane obtained by setting B, the breath speed, to zero.
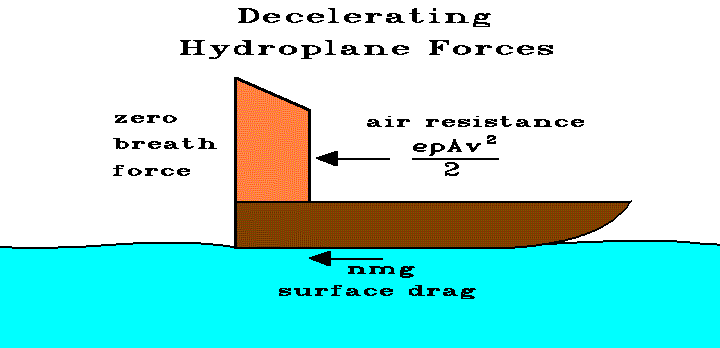
The deceleration of a hydroplane can be modeled using the general model for a vehicle undergoing terminated motion . The equation of motion can be written grossly as,
ma = - R - D
This is not a balance equation. Surface sliding drag and sail resistance depend on the existence of the driving force that accelerates the boat and soon reduce to zero when it is absent.
The force of friction due to sliding friction against a hydroplaning boat is caused by the weight, W, of the boat pushing down on the water surface. It is important to note that this model is only valid down to a certain speed at which the surface dynamic of the water can no longer support the boat and it sinks down into the water. In the water, pressure drag takes over as in the model of a coasting catamaran. But while the boat is hydroplaning, we write
D = nW where n is the sliding friction coefficient. The Weight, W, can also be written mg.
The force on the sail is zero, since blowing has ceased.
As the boat slows down, air continues to resist the movement of the boat.
R = epAv2/2 where e is the pressure drag coefficient, p is the air density (the boat is still in the air), A is the front cross-sectional area of the whole boat and v is the speed of the air which is the speed of the boat.
Putting these together with the signs of slowing force terms made negative we get:
Force = Sail Force - Frictional Forces
Air Water
ma = 0 - epAv2/2 - nmg
We can now make the proper mapping between the physical factors of this model and those of the general one in the following table.
| General Model | This Model |
|---|---|
| M | m |
| k | epA/2 |
| Ds | nmg |
| v0 | v0 |
| L | L |
| t | t |
Using this map we can apply the general model results to this specific model without having to derive the expressions all over again. Instead, the general model expressions are rewritten using the corresponding expression noted in the map table above. Then the expressions are simplified a bit to give the specific expressions we seek for this model. If any additional expressions are needed for this model, they are derived below.
The various factors above are related to one another using physical laws and analysis. Some of these relationships have special meaning in understanding the model. These as well as kinematic factors (like time, acceleration, speed and distance) are recorded in the next table as a summary of the model.
| Description | Units | Expression |
|---|---|---|
| Equations of Motion | oz | ma = - nmg - epAv2/2 |
| Displacement Distance | in | Y = 2m/epA |
| Initial Velocity | in/s | v0 = vt \[1-exp(-2(y+y0)/Y)] from acceleration model v(y) |
| Momentum Transfer | ozs/in | P = \[epAnmg/2] |
| Displacement Time | s | T = m/P |
| Coasting Time | s | tc = T arctan(v0/V) |
| Matching Velocity | in/s | V = \[2nmg/epA] |
| Coasting Distance | in | yc = Y ln(\[1+v02/V2]) |
| Time | s | t(y) = tc - T arccos(exp((y-yc)/Y)) |
| Velocity | in/s | v(y) = V \[exp(-2(y-yc)/Y)-1] |
| Velocity | in/s | v(t) = V tan((tc-t)/T) |
| Distance | in | y(t) = y(t) = yc + Y ln(cos((tc-t)/T)) |
| Acceleration | in/s2 | a(t) = -ng/cos2((tc-t)/T) |
| Surface Drag Coefficient | scalar | n(e) = epAV2/2mg |
| Aerodynamic Drag Coefficient | scalar | e(n) = 2nmg/pAV2 |
|
Back to the Dry Dock |
| [Dry Dock] | [Title Page] |
| Raingutter Boat Racing - | Breathing Life Into Your Boat |
| Copyright © 1997, 2000, 2002, 2004 by Michael Lastufka, All rights reserved worldwide. | |